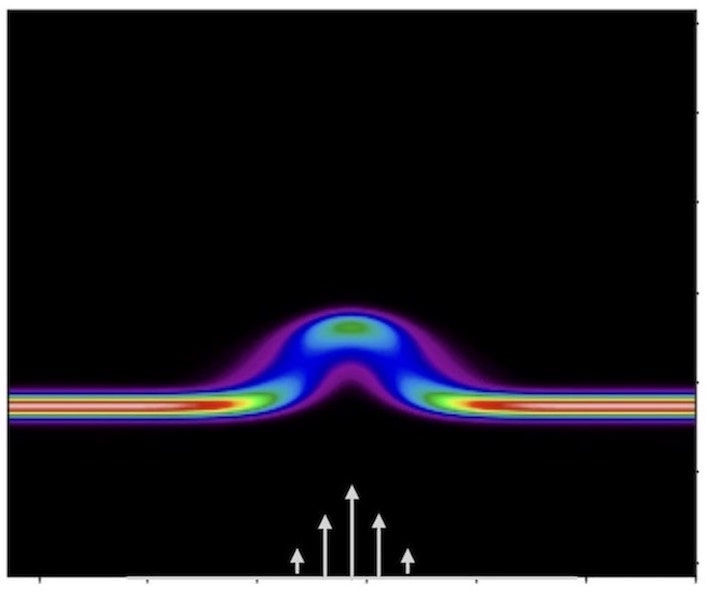
Assistant Research Scientist Miguel Jiménez-Urias has published a paper on the dispersion of passive tracer. The title is “On the non-self-adjoint and multiscale character of passive scalar mixing under laminar advection” and the paper appears in the Journal of Fluid Mechanics.
Miguel writes in the paper’s Abstract:
“Except in the trivial case of spatially uniform flow, the advection-diffusion operator of a passive scalar tracer is linear and non-self-adjoint. In this study, we exploit the linearity of the governing equation and present an analytical eigenfunction approach for computing solutions to the advection-diffusion equation in two dimensions given arbitrary initial conditions, and when the advecting flow field at any given time is a plane parallel shear flow. Our analysis illuminates the specific role that the non-self-adjointness of the linear operator plays in the solution behavior, and highlights the multiscale nature of the scalar mixing problem given the explicit dependence of the eigenvalue-eigenfunction pairs on a multiscale parameter q=2ikPen, where k is the non-dimensional wavenumber of the tracer in the streamwise direction and Pen is the Péclet number. We complement our theoretical discussion on the spectra of the operator by computing solutions and analyzing the effect of shear flow width on the scale-dependent scalar decay of tracer variance, and characterize the distinct self-similar diffusive processes that arise from the shear flow dispersion of an arbitrarily compact tracer concentration. Lastly, we discuss limitations of the present approach and future directions.”
Miguel was supported by the Poseidon Project and an IDIES Seed Fund Award during this research.